About Page
General Notes
Whatever year you are in, read everything before your section as well.
If text is highlighted, that refers to text that you would be typing.
If you want to communicate your actuarial expression, use your expression for example 1000a20| + 50A50.
If the bot does not respond then your request did not have the format required from this page. It should respond with an image with the final answer.
Spaces don’t matter. It will read a [12] 10| at i=4% exactly the same as a[12]10|ati=4%.
All numbers specifying the actuarial functions must be integers.
You should use * to describe multiplication if you are multiplying two actuarial terms together. In almost every other case, the symbol is not required.
Most of the program is case sensitive. The biggest reason for this is to distinguish a and A.
First Year
Interest Rate
The default interest rate is i = 4% p.a. If you want to use something else, put at i=5% directly after your actuarial term. For example a10| at i=5%. You can specify at i=0.05 too. Or i=5% without the “at”.
Vn
Vn does not exist. Rather use An|. This will give the same input to the bot. For example A10| gives:
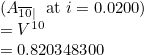
Annuities
Both “round a” and “S” are valid inputs. To describe “angle n” to the bot, use n| directly after the symbol. For example S10| will give the following output:
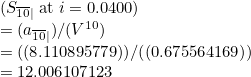
Note that any form of “S” will always be calculated in terms of “round a” first.
Deferred Annuities
To describe a deferment period of d, you must put d| in front of the symbol. For example 10|a20| describes the PV of an annuity of 1 p.a. payable in arrears from time 10 to time 30. Its solution:
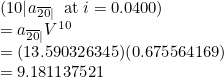
Continuous And Advance Annuities
To describe a continuous annuity, put an underscore: _ in front of the symbol (after the deferment period). For example 10|_a20| describes the same set of payments as above but payments are now continuous.
To describe an advance annuity, put a comma: , in front of the symbol (after the deferment period). For example 10|,a20| describes the same set of payments as above but payments are now in advance.
Perpetuities
To describe an annuity payable for ever, leave out the term. For example _a i=0.06 gives the following:
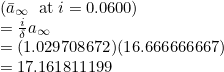
Note that if the entire expression results in a single character, a, this will produce an error and so to correct this, just specify the interest rate at the end.
Annuities Payable pthly
To describe an annuity payable p times per annum, put square brackets, [p] directly after the symbol. For example ,S[12]10| i=5% will produce the following output:
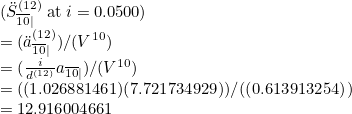
The bot will use the i/i(p) method instead of a change in interest rate method.
The most common error is likely to be here. You MUST remember to use square brackets.
Large Example
Applying all explained here, and to show off the variety of ways to express what you want, the following can be inputted:
500(A10| i=5%) + 10(10|_a5| at i=10%)*(S[12]10|) + 20(a at 0.07)
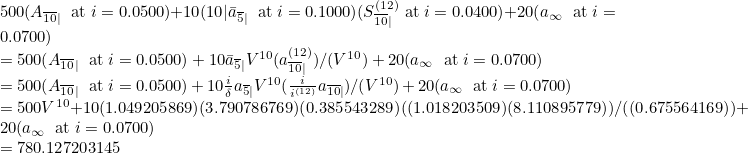
What The Bot Can’t Do
The bot cannot do (Ia), (Da), (IS) or (DS).
Second Year
Life Tables
The default mortality used is AM92 however there are also PMA92C20 and PFA92C20 tables that the bot can use. Note that AM92 Select mortality tables cannot be used yet.
The mortality is specified in basically the same way as the interest: at the end of everything and it is specified for each symbol. To specify 4% AM92, write at i=4% AM92 or i=4% am92 or just am which also takes advantage of the 4% default interest rate. Similarly PFA92C20 or pfa92c20 or pfa can specify PFA mortality. Similarly for PMA. Note that Am92, Am, Pfa, PMA92c20 are all invalid since the case must be the same throughout.
Annuities
A whole life annuity for a life aged x is specified with ax. Advance, continuous and pthly payments are all described above. For example ,a[12]50 will be at 4% AM92 and the output is:
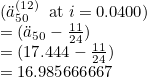
A termed annuity for a life aged x with term n is ax:n|. So for example, _a60:20| PMA gives:
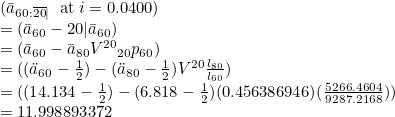
Note that it only uses whole life values from the tables and derives all termed values.
Assurances
A whole life assurance for a life aged x is specified with Ax. If death is payable immediately then treat it the same as a continuous assurance: put an underscore before the “A”. For example A55 i=4% PFA is:
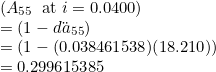
If the number cannot be directly taken from the table, it uses other related values.
A termed endowment assurance for a life aged x with term n is Ax:n|. So for example, _A60:20| i=8.16% PMA gives:
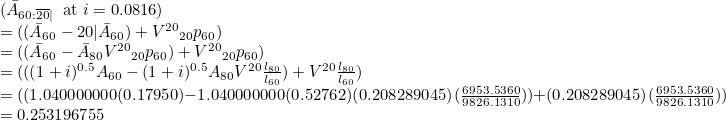
Its method is not always the most efficient for assurances.
A termed endowment assurance for a life aged x with term n is Ax.:n|. That is, a full stop is placed just after the “x” and before the “:”. For example, A20.:20| gives:
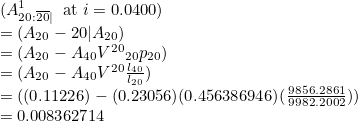
A pure endowment is expressed a similar way: Ax:n.| with a full stop before “n” and after the “|”. For example A20:20.| gives:
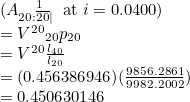
What The Bot Can’t Do
The bot cannot do (Ia)x or (IA)x.
Third Year
Joint Life Annuities
These should work as you expect. The male life is always on the left and the female life is always on the right. The mortality is always PMFA92C20 and it is always first-death. The interest rate is always i=4%. If you specify anything else, you might get nonsensical answers.
For example, ,a[12]50:50:10| gives:
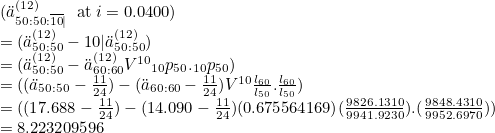
Note that the minimum age of the male is 50 and there cannot be an absolute difference between the (x) and (y) of 20. I.e. |x-y|<=20. This applies for assurances as well.
Joint Life Assurances
The mortality is always PMFA92C20 and it is always first-death.
For a endowment assurance for lives aged x and y for a term of n years, we have Ax:y:n|. For example, A60:50:10| gives:
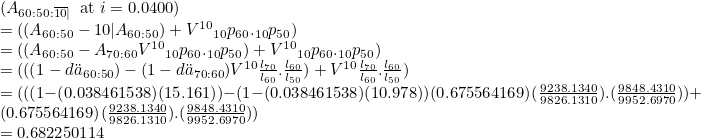
For a term assurance, we have Ax.:y:n| or Ax:y.:n| or Ax.:y.:n|. The full stop just needs to be on at least one of the lives. For example, A50.:60:10| gives:
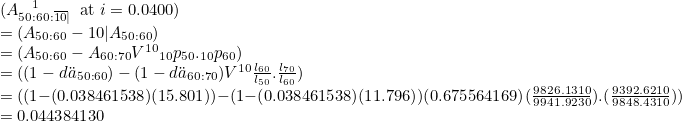
For an endowment assurance, we have Ax:y:n.| so the full stop must be just after the “n” and before the “|”. For example A50:60:10.| gives:
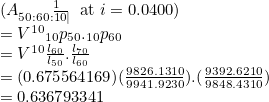
What The Bot Can’t Do
It cannot do last death functions. You must simplify the problem first to obtain single life and joint first life functions.
It cannot do reversionary annuities. Again your problem must be simplified to single life and join first life annuities. I’m too lazy to add this feature.
If you find any problems or any incorrect answers, please send me a message on this forum.
Hi There
Thanks for vising. Hope you enjoy your stay. If you wish to comment, please sign up or log in and verify your account.